The Morphohedron and The Art of Golden Geometry
The Morphohedron is the combination of all the known possible Regular Polyhedrons, both the five Platonic Solids and the 4 Kepler-Poinsot figures. They fit together in a special sequence, in three dimensions, just as the Fibonacci sequence does numerically in one dimension. Each configuration is larger than its predecessor by 1.618, the famous Golden Ratio. Thus, starting with an icosahedron at the center, and then 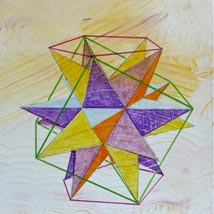 stellating it (lengthening each face by 1.618 ), you will have the verticies of a dodecahedron, which in its turn, can be stellated to produce a larger version of the icosahedron. This process can continue ad infinitum, in either direction, larger or smaller. That accounts for 4 of the 9 possible regular 3 dimensional figures. The Cube is formed by connecting 8 of the 20 verticies of the stellated icosahedron. The Tetrahedron is formed by the diagonals of that cube, and the octahedron is formed by connecting the midpoints of that Tetrahedron. This accounts for 3 more regular figures, or polyhedra. The remaining regular 3-dimensional figures,are the two Pointsot Figures, which are concave versions of the dodecahedron and the icosahedron, and will fit in the same shell as their convex versions. Since all the possible Regular Solids will fit within this sequence, morphing from one form into the other endlessly, we are led to consider them as a unified system, rather than 9 separate, discrete objects.
stellating it (lengthening each face by 1.618 ), you will have the verticies of a dodecahedron, which in its turn, can be stellated to produce a larger version of the icosahedron. This process can continue ad infinitum, in either direction, larger or smaller. That accounts for 4 of the 9 possible regular 3 dimensional figures. The Cube is formed by connecting 8 of the 20 verticies of the stellated icosahedron. The Tetrahedron is formed by the diagonals of that cube, and the octahedron is formed by connecting the midpoints of that Tetrahedron. This accounts for 3 more regular figures, or polyhedra. The remaining regular 3-dimensional figures,are the two Pointsot Figures, which are concave versions of the dodecahedron and the icosahedron, and will fit in the same shell as their convex versions. Since all the possible Regular Solids will fit within this sequence, morphing from one form into the other endlessly, we are led to consider them as a unified system, rather than 9 separate, discrete objects.
The fact that they all relate to each other by way of the Golden Ratio, or the Extreme and Mean Ratio, makes it even more interesting, and curious.
The Morphohedron, like all the regular solids, is a three dimensional phenomenon, yet it can be pictured in two dimensional drawings by orthogonal projection, just as the sun at noon projects the shadow of an object on the flat ground. (at noon the rays of light are perpendicular to the ground.) The shadow of the Morphohedron also demonstrates the Golden Ratio, and leads to speculation that this 3-d Morphohedron could be the orthogonal projection of regular figures in 4 or more dimensions. It could also be the geometry of sub-nuclear quantum mechanics.
Being an architect, I use orthogonal projection every time I draw a floor plan or exterior elevation of a house or building. These drawings do not exhibit perspective, and therefore can be accurately measured by their builders. After building three dimensional models, or sculptures, of the Morphohedron, I began making orthogonal drawings and paintings from several different angles, or points of view. These are the images seen on this website, which demonstrate the symmetry and variety of the Morphohedron.
Many artbooks attempt to analyze famous paintings and buildings to discover the Golden Ratio hidden inside. In these Morphohedron paintings, there is no need to wonder, they are all completely ruled by this “Divine Proportion”. View and enjoy the paintings on this website, and for more complete explanations, see my forthcoming book; “ Morphohedron, the Art of Golden Geometry”.




